PyTorch_《Deep learning with PyTorch》

路漫漫其修远兮。本篇章主要记录的是清华翻译的《Deep learning with PyTorch》这本书中的重要内容，是Pytorch探索之旅的第1篇章！

Reference materials include:

• 清华翻译的《Deep learning with PyTorch》

1. Introduction

PyTorch是一个使用Python格式实现深度学习模型的库。它的核心数据结构Tensor，是一个多维数组。Pytorch就像是一个能在GPU上运行并且自带自动求导功能的Numpy数组。它配备了高性能的C++运行引擎使得他不必依赖Python的运行机制：

• Pytorch的很大部分使用C++和CUDA（NVIDIA提供的类似C++的语言）编写。
• PyTorch核心是提供多维数组（tensor）的库， torch模块提供了对其进行扩展操作的库。
• 同时PyTorch的第二个核心功能是允许Tensor跟踪对其所执行的操作，并通过反向传播来计算输出相对于其任何输入的导数。

PyTorch最先实现了深度学习架构，深度学习模型强大的原因是因为它可以自动的学习样本输出与所期望输出之间的关系。

1.1 PyTorch提供了构建和训练神经网络所需的所有模块：

• 构建神经网络的核心模块位于troch.nn中。包括全连接层、卷积层、激活函数和损失函数。
• torch.util.data能找到适用于数据加载和处理的工具，相关的两个主要的类为Dataset和DataLoader。
  - Dataset承担了自定义的数据格式与标准的Pytorch张量之间的转换任务
  - DataLoader可以在后台生成子进程来从Dataset中加载数据，使数据准备就绪并在循环可以使用后立即等待训练循环
  - 除此之外还可以使用专用的硬件（多个GPU）来训练模型，在这些情况下，可以通过torch.nn.DataParallel和torch.distributed来使用其他的可用硬件

Pytorch使用Caffe2作为后端，增加了对ONNX的支持（定义了一种与深度学习库无关的模型描述和转换格式），增加了称为TorchScript的延迟执行图模式运行引擎（这个模块避开了Python解释器所带来的成本，我们可以将这个模型看作是具有针对张量操作的有限指令集的虚拟机，它的调用不会增加Python的开销，还能使PyTorch可以实时地将已知序列转换为更有效的混合操作）。默认的运行方式是即使执行（eager mode）。

关于PyTorch的安装，windows建议使用Anaconda，Linux建议使用Pip。

2. 从张量开始

- Tensor是Pytorch最基本的数据结构

深度学习的应用往往是将某种形式获取的数据（图像或文本）转换为另一种形式的数据（标签、数字或文本），因此从这个角度看，深度学习就像是构建一个将数据从一种表示转换为另一种表示的系统，这种转换是通过从一系列样本中提取共性来驱动的额，这些共性能够反映期望的映射关系。
为了实现上述过程，首先需要让网路理解输入数据，因此输入需要被转换为浮点数的集合。这些浮点数的集合及其操作是现代AI的核心。而网络层次之间的数据被视为中间表示（intermediate representation）。中间表示是将输入与前一层神经元权重相结合的结果，每个中间表示对于之前的输入都是唯一的。
为此，PyTorch引入了一个基本的数据结构：张量（tensor）。张量是指将向量（vector）和矩阵（matrix）推广到任意维度，与张量相同概念的另一个名称是多维数组（multidimensional array）。

2.1 张量基础

Python列表或数字元组（tuple）是在内存中单独分配的Python对象的集合；而PyTorch张量或NumPy数组（通常）是连续内存块上的视图（view），这些内存块存有未封装（unboxed）的C数值类型。
获取一个张量的形状：tensor.shape

2.2 张量与存储

基础内存只分配一次，由torch.Storage实例管理，Storage是一个一维的数值数据数组，例如一块包含了指定类型（可能是float或int32）数字的连续内存块。而tensor可以看作是某个Storage实例的视图。因此多个tensor可以索引到同一Storage。

import torch
points = torch.tensor([[1.0, 4.0], [2.0, 1.0], [3.0, 5.0]])
points.storage()

# 输出
 1.0
 4.0
 2.0
 1.0
 3.0
 5.0
[torch.FloatStorage of size 6]

无法使用两个索引来索引二维tensor的存储，因为Storage始终是一维的，与引用它的任何张量的维数无关。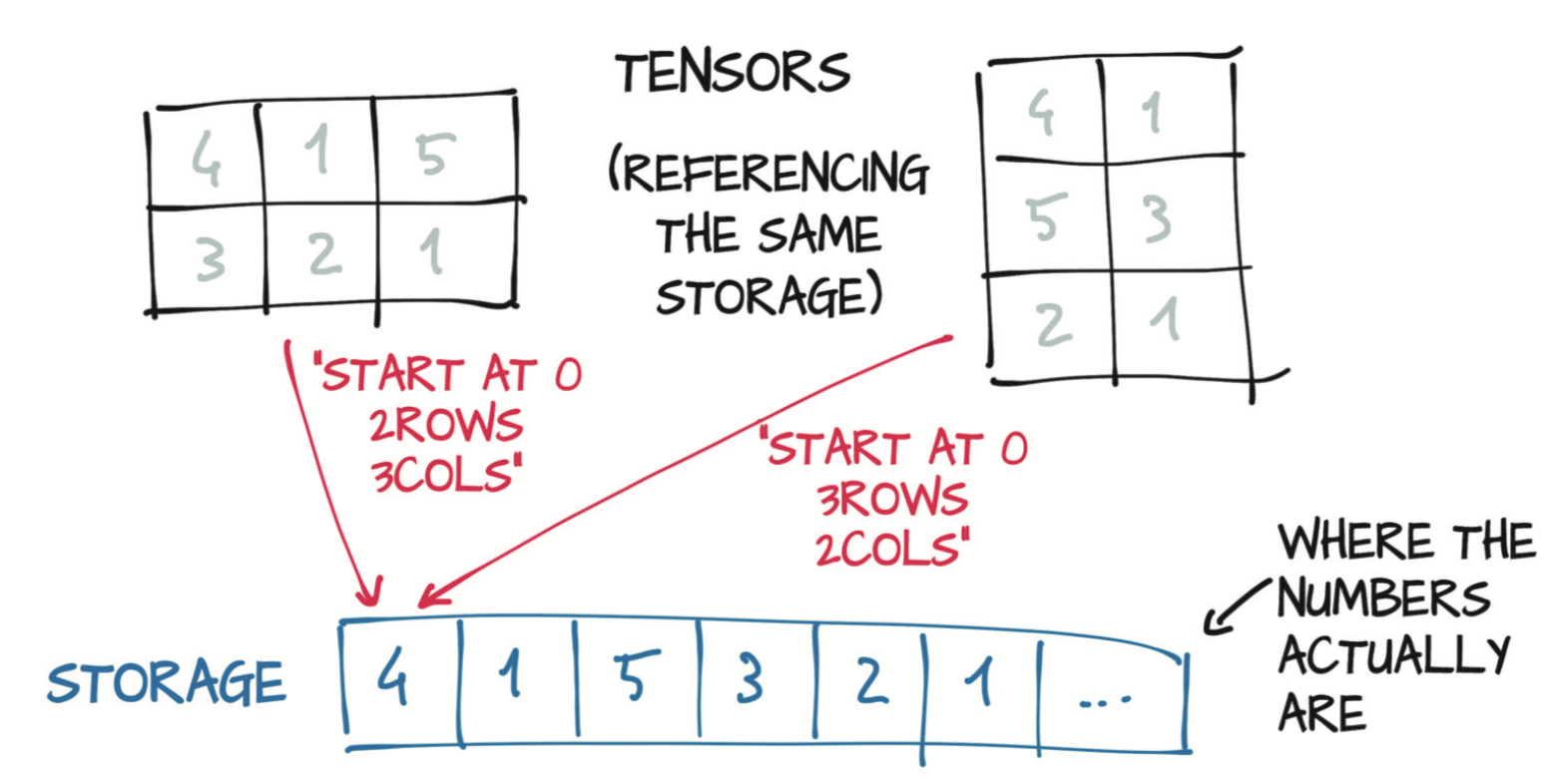

2.3 尺寸、存储偏移与步长

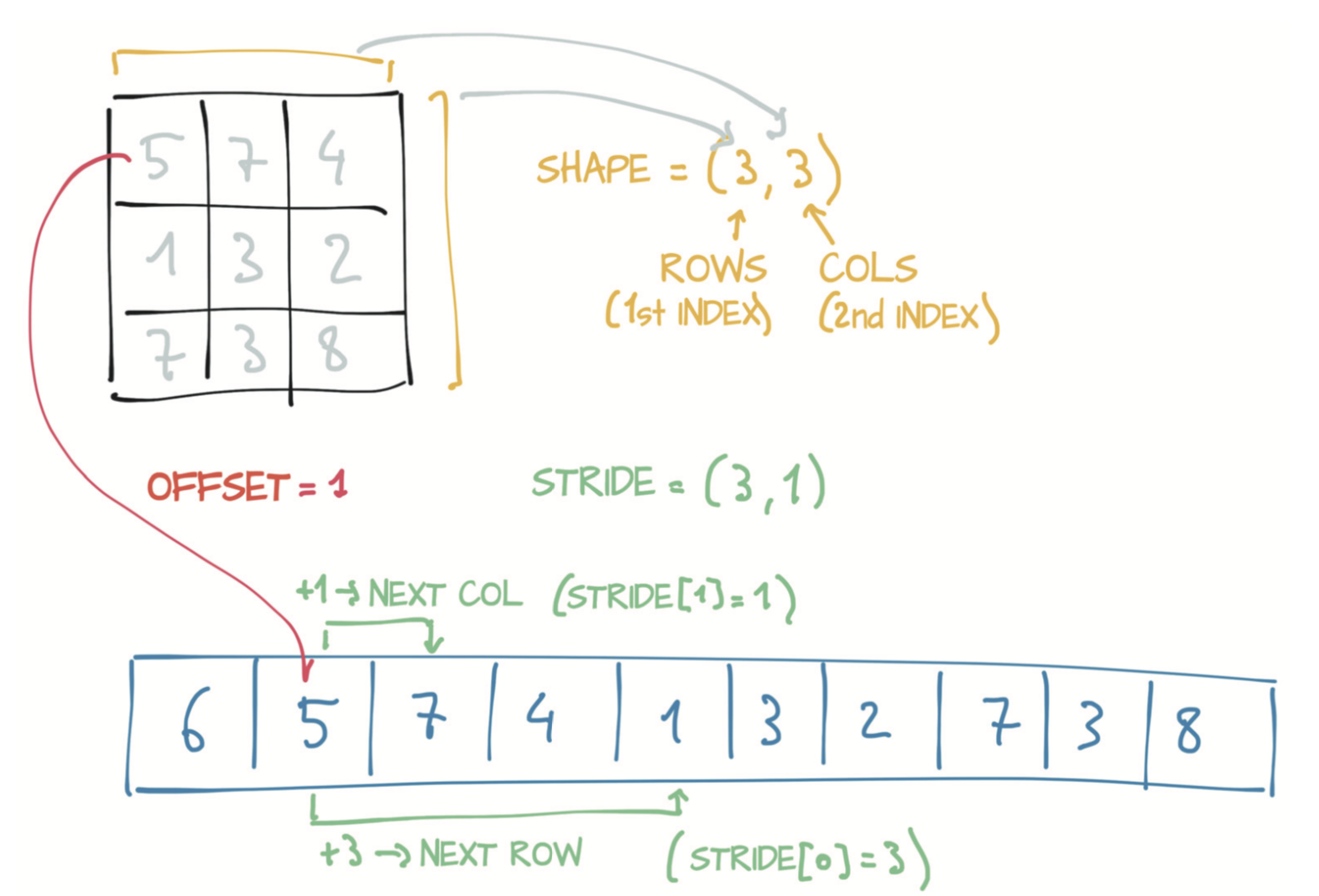
tensor可以看作是某个Storage实例的视图。为了索引Storage，张量依赖于几条明确定义它们的信息：尺寸（size）、存储偏移（storage offset）和步长（stride）
- 尺寸是一个元组，表示tensor每个维度上有多少个元素。
- 存储偏移是Storage中与张量中的第一个元素相对应的索引。
- 步长是在Storage中为了沿每个维度获取下一个元素而需要跳过的元素数量。
- 步长是一个元组，表示当索引在每个维度上增加1时必须跳过的存储中元素的数量。
- shape是属性，size()是类，这俩包含的信息相同。

用下标i和j访问二维张量等价于访问存储中的storage_offset + stride[0] * i + stride[1] * j元素。
张量Tensor和和存储Storage之间的这种间接操作会使某些操作（例如转置或提取子张量）的代价很小，因为它们不会导致内存重新分配；相反，它们（仅仅）分配一个新的张量对象，该对象具有不同的尺寸、存储偏移或步长。更改子张量同时也会对原始张量产生影响。所以我们可以克隆子张量得到新的张量（以避免这种影响）：tensor.clone().Tensor的转置只改变尺寸和步长。

some_tensor = torch.ones(3, 4, 5)
some_tensor.shape, some_tensor.stride()
# 输出
(torch.Size([3, 4, 5]), (20, 5, 1))

some_tensor_t = some_tensor.transpose(0, 2)
some_tensor_t.shape, some_tensor_t.stride()
# 输出
(torch.Size([5, 4, 3]), (1, 5, 20))

2.4 数据类型

• torch.float32/torch.float —— 32位浮点数:torch.FloatTensor = torch.Tensor
• torch.float64/torch.double —— 64位双精度浮点数:torch.DoubleTensor
• torch.float16/torch.half —— 16位半精度浮点数
• torch.int8 —— 带符号8位整数:torch.CharTensor
• torch.uint8 —— 无符号8位整数:torch.ByteTensor
• torch.int16/torch.short —— 带符号16位整数
• torch.int32/torch.int —— 带符号32位整数
• torch.int64/torch.long —— 带符号64位整数

通过访问dtype属性来获得张量的数据类型。而数据类型之间的转换可以通过type和to实现：

short_points = torch.ones(10, 2).short()
short_points = torch.ones(10, 2).to(dtype=torch.short)

2.5 索引张量

some_list = list(range(6))
some_list[:]     # 所有元素
some_list[1:4]   # 第1（含）到第4（不含）个元素
some_list[1:]    # 第1（含）个之后所有元素
some_list[:4]    # 第4（不含）个之前所有元素
some_list[:-1]   # 最末尾（不含）元素之前所有元素
some_list[1:4:2] # 范围1（含）到4（不含），步长为2的元素

points[1:]    # 第1行及之后所有行，（默认）所有列
points[1:, :] # 第1行及之后所有行，所有列
points[1:, 0] # 第1行及之后所有行，仅第0列

2.6 Pytorch与NumPy的互通性

从PyTorch张量创建NumPy数组：points_np = points.numpy()
从NumPy数组创建PyTorch张量：points = torch.from_numpy(points_np)

2.7 序列化张量

PyTorch内部使用pickle来序列化张量对象和实现用于存储的专用序列化代码。

# 将points张量保存到ourpoints.t文件中
torch.save(points, '../../data/chapter2/ourpoints.t')
# 将points加载回来
points = torch.load('../../data/chapter2/ourpoints.t')

## 上述例子可让你快速保存张量，但这个文件格式本身是不互通的，你只能用PyTorch读取它
## 对于需要（互通）的情况，你可以使用HDF5格式和库
## HDF5是一种可移植的、广泛支持的格式，用于表示以嵌套键值字典形式组织的序列化多维数组。
## Python通过h5py库支持HDF5，该库以NumPy数组的形式接收和返回数据。

import h5py

f = h5py.File('../../data/chapter2/ourpoints.hdf5', 'w')
dset = f.create_dataset('coords', data=points.numpy())
f.close()
# coords是传入HDF5文件的键值
# 你可以索引在磁盘的数据并且仅访问你感兴趣的元素，例如你只想加载数据集中的最后两个点数据：
f = h5py.File('../../data/chapter2/ourpoints.hdf5', 'r')
dset = f['coords']
last_points = dset[1:]

2.8 将张量转移到GPU上运行

PyTorch张量还具有设备（device）的概念，这是在设置计算机上放张量（tensor）数据的位置。

• 通过为构造函数指定相应的参数，可以在GPU上创建张量：points_gpu = torch.tensor([[1.0, 4.0], [2.0, 1.0], [3.0, 4.0]], device='cuda')；同时可以通过提供device和dtype参数来同时更改位置和数据类型
• 也可以使用to方法将在CPU上创建的张量（tensor）复制到GPU：points_gpu = points.to(device='cuda')
• 使用速记方法cpu和cuda代替to方法来实现相同的目标：points_gpu = points.cuda(0)和points_cpu = points_gpu.cpu()

3 使用张量表示真实数据

将异构的现实世界数据编码成浮点数张量以供神经网络使用。

• 表格数据：表格中的每一行都独立于其他行，他们的顺序页没有任何关系
• 时间序列：存在严格的排序其他类型的数据。比如文本和音频。
• 文本数据：将文本信息编码为张量形式的技术为独热编码。
  每个字符将由一个长度等于编码中字符数的向量表示。该向量除了有一个元素是1外其他全为0，这个1的索引对应该字符在字符集中的位置。接下来，在编码中建立单词到索引的映射，一般单词作为键，而整数作为值。独热编码时，你将使用此词典来有效地找到单词的索引。但由于独热编码不支持长篇文本，后续出现了嵌入的方式处理文本。
  【关于文本嵌入】
  用于同一上下文的单词映射到嵌入空间的邻近区域。生成的嵌入的一个有趣的方面是，相似的词不仅会聚在一起，还会与其他词保持一致的空间关系。如果你要使用“苹果”的嵌入向量，并加上和减去其他词的嵌入向量，就可以进行类比，例如苹果 - 红色 - 甜 + 酸，最后可能得到一个类似柠檬的向量。
• 图像数据：图像表示为按规则网格排列的标量集合。PyTorch模块处理图像数据需要将张量设置为C x H x W（分别为通道、高度和宽度）
• 体积数据：在CT（Computed Tomography）扫描等医学成像应用程序的情况下，通常需要处理从头到脚方向堆叠的图像序列，每个序列对应于整个身体的横截面。在CT扫描中，强度代表身体不同部位的密度：肺、脂肪、水、肌肉、骨骼，以密度递增的顺序排列，当在临床工作站上显示CT扫描时，会从暗到亮映射。根据穿过人体后到达检测器的X射线量计算每个点的密度，并使用一些复杂的数学运算将原始传感器数据反卷积（deconvolve）为完整体积数据。CT具有单个的强度通道，这类似于灰度图像。通过将单个2D切片堆叠到3D张量中，你可以构建表示对象的3D解剖结构的体积数据。

4 学习机制

数据科学的流程

• 得到很多好的数据
• 试图将这些数据可视化
• 选择有可能拟合数据的最简单的模型
• 划分数据，以便处理部分数据并保留独立的数据集用来验证
• 从试探性的偏心率和大小开始，然后进行迭代直到模型拟合观察结果为止
• 根据独立的数据集验证他的模型

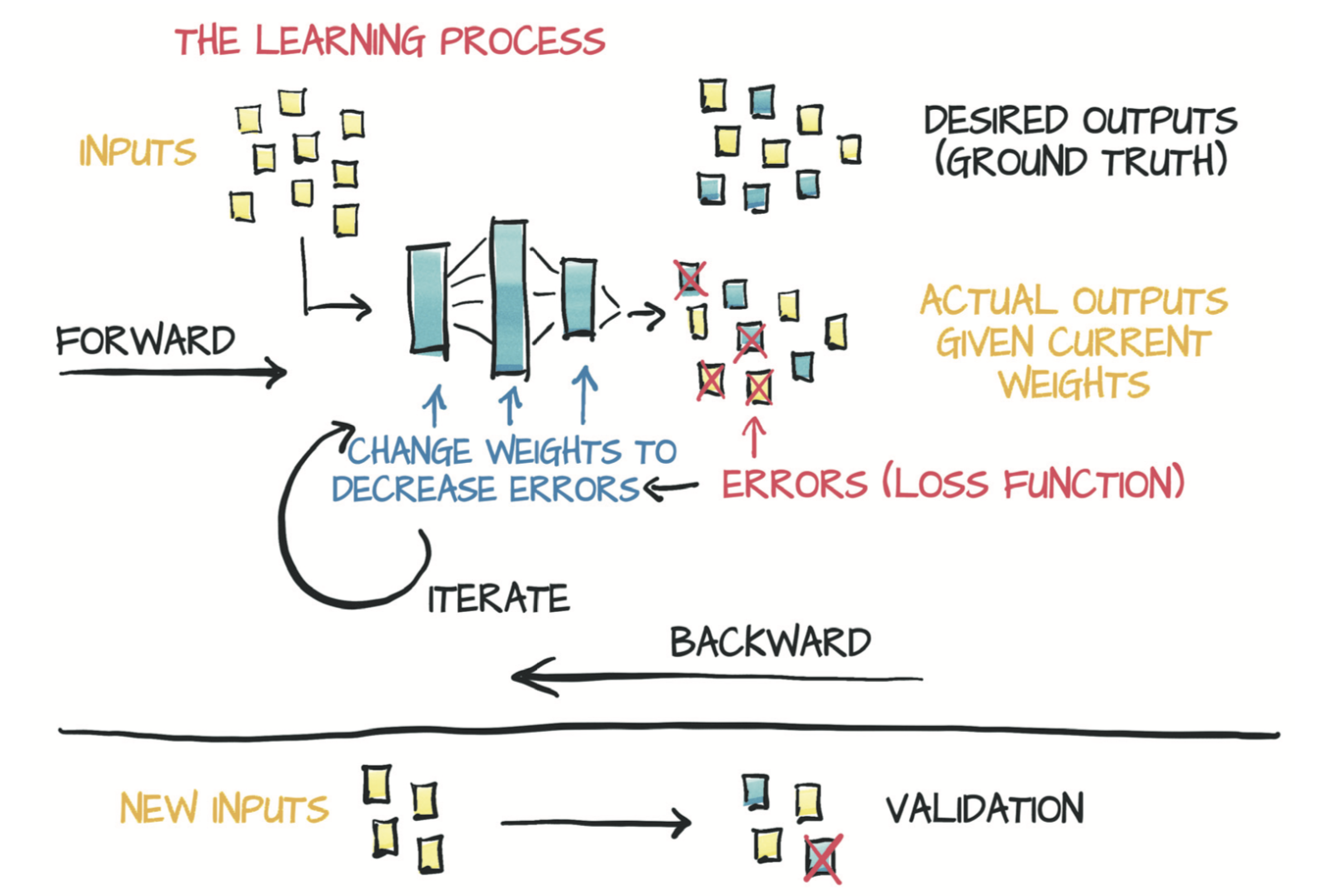
4.1 一个反向传播的简单示例

通过链式法则向后传播导数，可以计算复合函数（模型函数和损失函数）相对于它们的最内层参数w和b的梯度。基本的要求是涉及到的函数都是可微分的。

# 定义模型
def model(t_u, w, b):
    return w * t_u + b

# 定义损失函数
def loss_fn(t_p, t_c):
    squared_diffs = (t_p - t_c)**2
    return squared_diffs.mean()

# 导数
def dmodel_dw(t_u, w, b):
    return t_u

def dmodel_db(t_u, w, b):
    return 1.0

# 返回相对于 w 和 b 的梯度的函数
def grad_fn(t_u, t_c, t_p, w, b):
    dloss_dw = dloss_fn(t_p, t_c) * dmodel_dw(t_u, w, b)
    dloss_db = dloss_fn(t_p, t_c) * dmodel_db(t_u, w, b)
    return torch.stack([dloss_dw.mean(), dloss_db.mean()])

# 循环训练
def training_loop(n_epochs, learning_rate, params, t_u, t_c, 
                    print_params = True, verbose=1):
    for epoch in range(1, n_epochs + 1):
        w, b = params

        t_p = model(t_u, w, b) # 前向传播
        loss = loss_fn(t_p, t_c)
        grad = grad_fn(t_u, t_c, t_p, w, b) # 反向传播

        params = params - learning_rate * grad

        if epoch % verbose == 0:
            print('Epoch %d, Loss %f' % (epoch, float(loss)))
            if print_params:
                print('    Params: ', params)
                print('    Grad  : ', grad)
    return params

4.2 Pytorch自动求导

一般来讲，所有PyTorch张量都有一个初始为空的名为grad的属性:params.grad is None # True。你可以将包含任意数量的张量的require_grad设置为True以及组合任何函数。在这种情况下，PyTorch会在沿着整个函数链（即计算图）计算损失的导数，并在这些张量（即计算图的叶节点）的grad属性中将这些导数值累积（accumulate）起来。
!!!!【Attention】
重复调用backward会导致导数在叶节点处累积。因此，如果提前调用了backward，然后再次计算损失并再次调用backward（如在训练循环中一样），那么在每个叶节点上的梯度会被累积（即求和）在前一次迭代计算出的那个叶节点上，导致梯度值不正确。为防止这种情况发生，你需要在每次迭代时将梯度显式清零:

if params.grad is not None:
    params.grad.zero_()

torch模块有一个optim子模块，你可以在其中找到实现不同优化算法的类。这里有一个简短的清单：

import torch.optim as optim
dir(optim)

# 输出
['ASGD',
 'Adadelta',
 'Adagrad',
 'Adam',
 'AdamW',
 'Adamax',
 'LBFGS',
 'Optimizer',
 'RMSprop',
 'Rprop',
 'SGD',
 'SparseAdam',
 ...
]

深度神经网络可以近似复杂的函数，前提是神经元的数量（即参数量）足够高。参数越少，网络能够近似的函数越简单。因此，这里有一条规律：如果训练损失没有减少，则该模型对于数据来说太简单了。另一种可能性是训练数据中不包含有意义的信息以用于预测输出。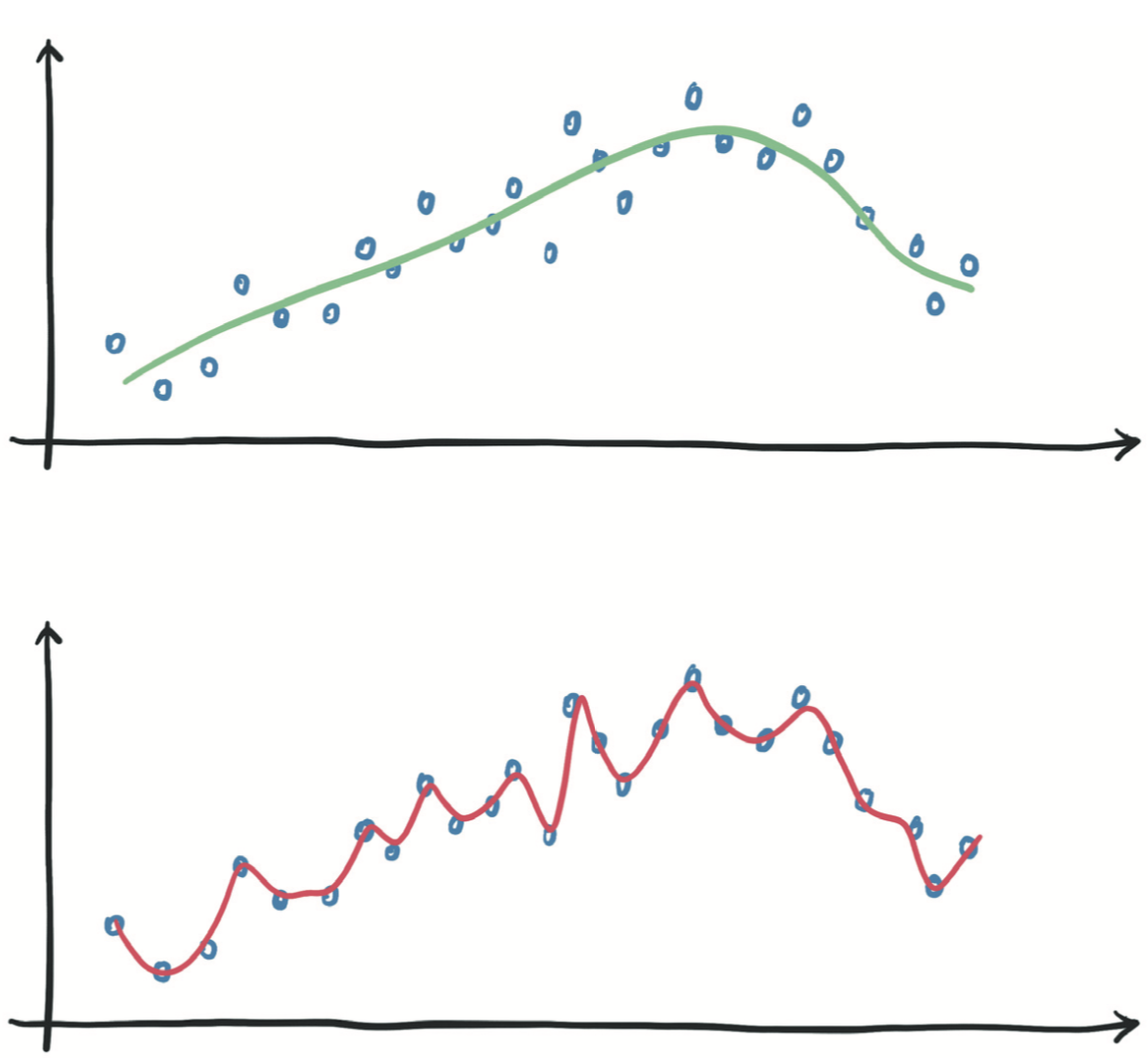

5 使用神经网络拟合数据

不管具体模型是什么，参数的更新方式都是一样的：反向传播误差然后通过计算损失关于参数的梯度来更新这些参数。神经网络具有非凸误差曲面主要是因为激活函数。组合神经元来逼近各种复杂函数的能力取决于每个神经元固有的线性和非线性行为的组合。深度神经网络可让你近似高度非线性的过程，而无需为它们建立明确的模型。

5.1 神经元

深度学习的核心是神经网络，即能够通过简单函数的组合来表示复杂函数的数学实体。这些复杂函数的基本组成单元是神经元，如图5.2所示。从本质上讲，神经元不过是输入的线性变换（例如，输入乘以一个数[weight，权重]，再加上一个常数[偏置，bias]），然后再经过一个固定的非线性函数（称为激活函数）。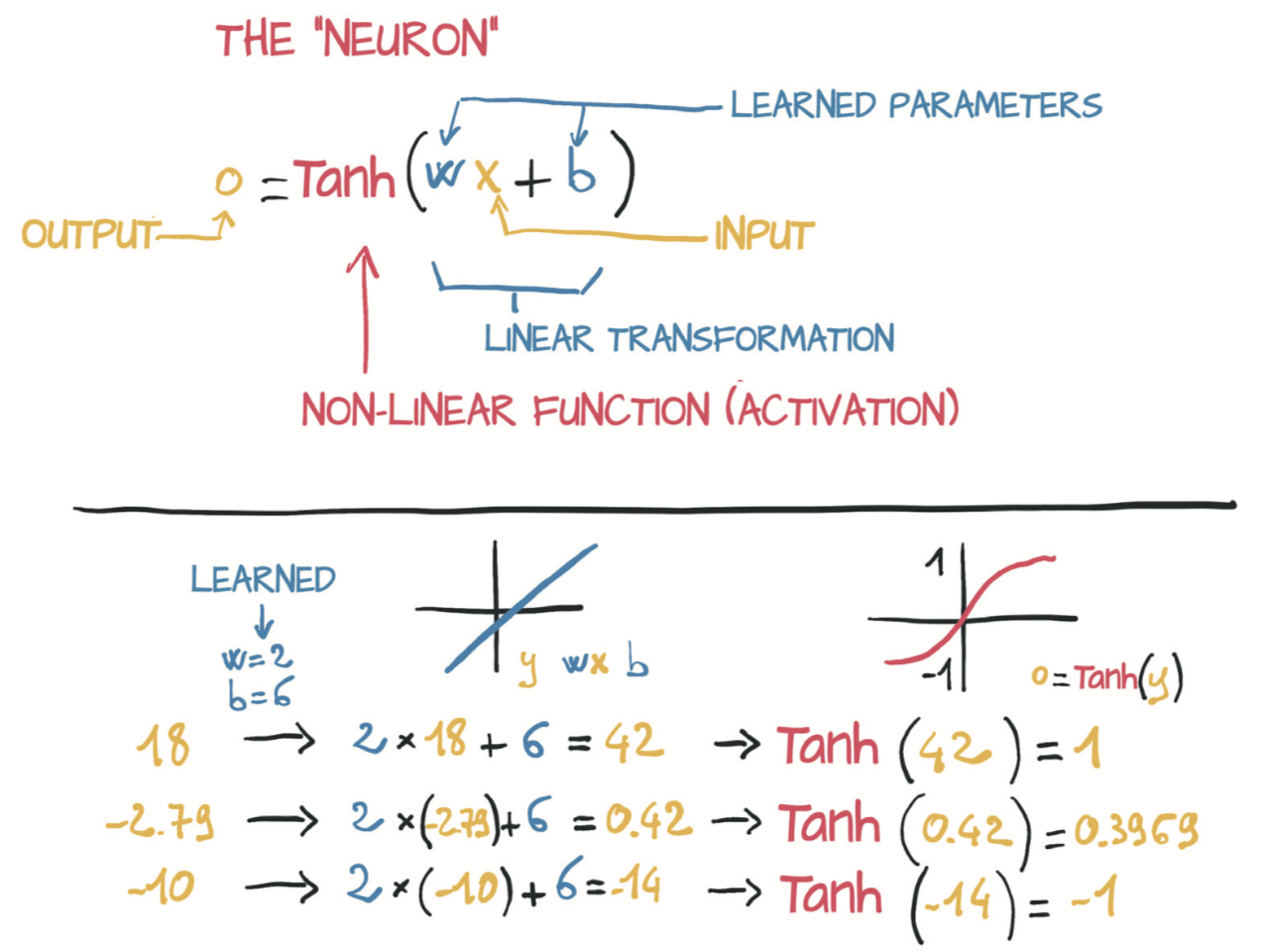

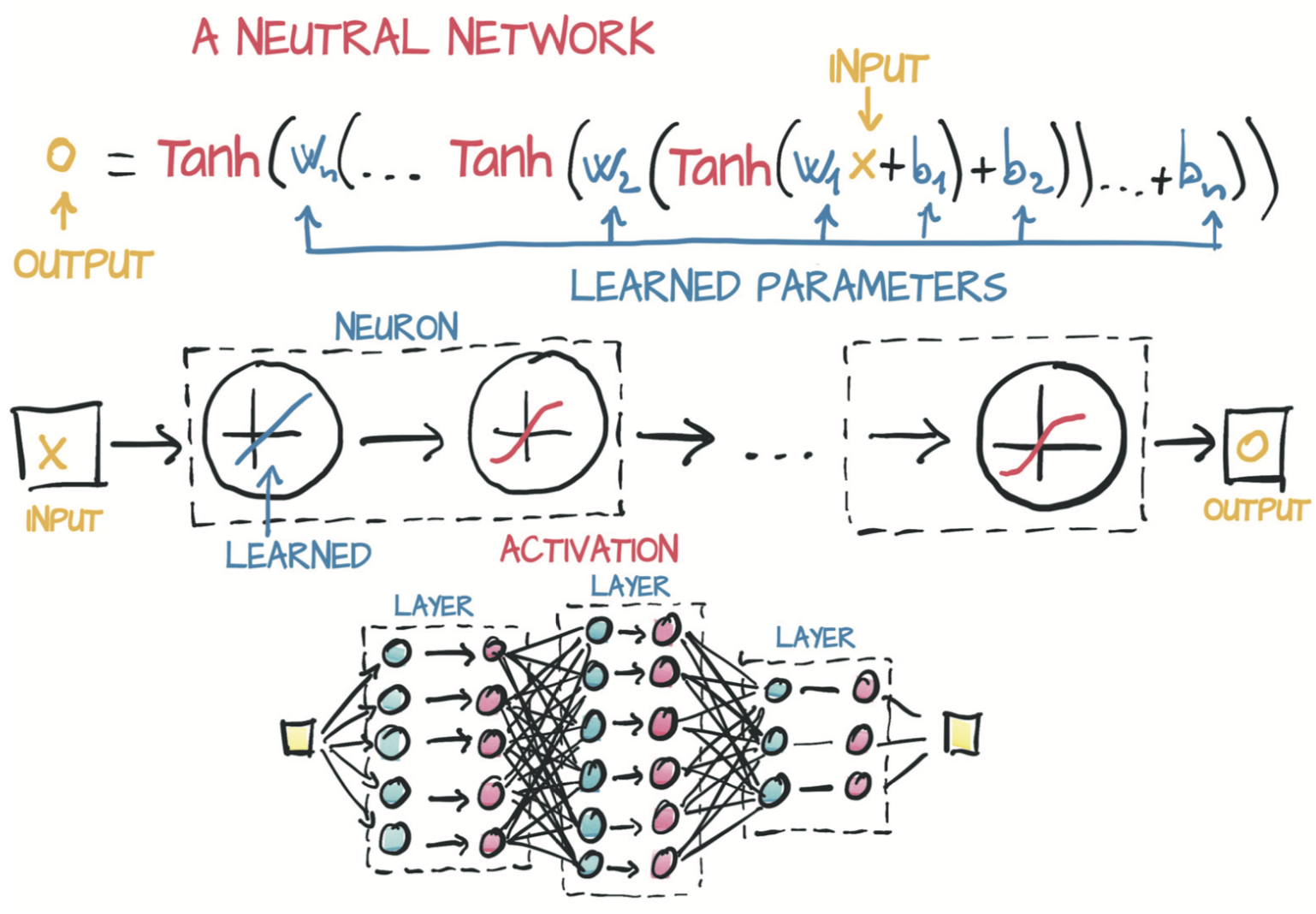
5.2 激活函数

激活函数的作用是将先前线性运算的输出聚集到给定范围内。一系列线性变换紧跟可微激活函数中可以构建出能近似高度非线性过程的模型，且可以通过梯度下降很好地估计出其参数。
激活函数的要求有：

• 非线性
• 可微
  

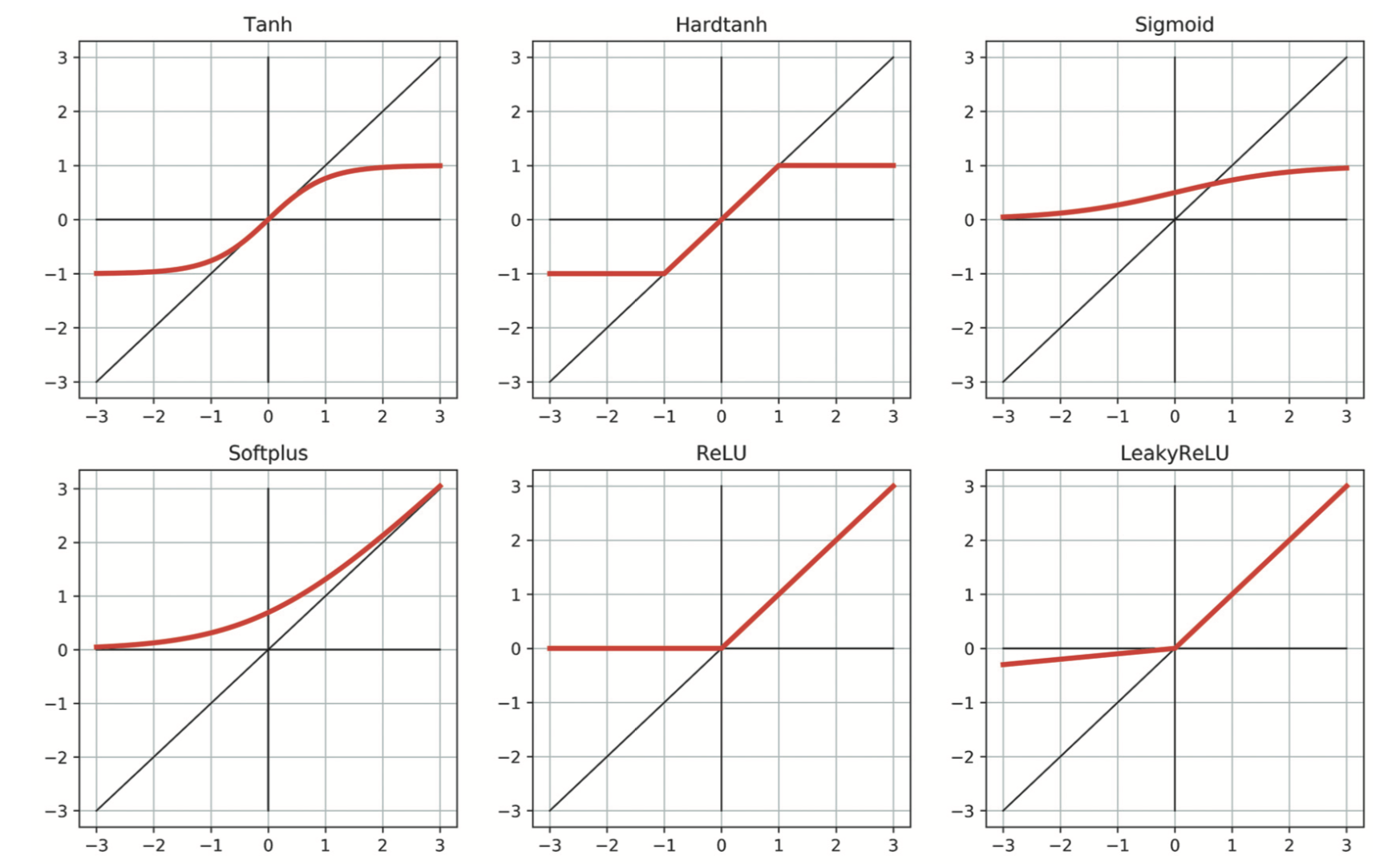
5.3 PyTorch的nn模块

PyTorch有一个专门用于神经网络的完整子模块：torch.nn。该子模块包含创建各种神经网络体系结构所需的构建块。这些构建块在PyTorch术语中称为module（模块），在其他框架中称为layer（层）。nn中的任何模块都被编写成同时产生一个批次（即多个输入）的输出。这样进行批处理的主要原因是希望可以充分利用执行计算的计算资源。

# 1. nn提供了一种通过nn.Sequential容器串联模块的简单方法
seq_model = nn.Sequential(
            nn.Linear(1, 13),
            nn.Tanh(),
            nn.Linear(13, 1))
seq_model
## 输出
Sequential(
  (0): Linear(in_features=1, out_features=13, bias=True)
  (1): Tanh()
  (2): Linear(in_features=13, out_features=1, bias=True)
)
# ——————————————————————————————————————————————————————————————————

## 1.1 Sequential中每个模块的名称都是该模块在参数中出现的顺序。
##      有趣的是，Sequential还可以接受OrderedDict作为参数
#       这样就可以给Sequential的每个模块命名
from collections import OrderedDict

seq_model = nn.Sequential(OrderedDict([
    ('hidden_linear', nn.Linear(1, 8)),
    ('hidden_activation', nn.Tanh()),
    ('output_linear', nn.Linear(8, 1))
]))

seq_model
## 输出
Sequential(
  (hidden_linear): Linear(in_features=1, out_features=8, bias=True)
  (hidden_activation): Tanh()
  (output_linear): Linear(in_features=8, out_features=1, bias=True)
)
# ——————————————————————————————————————————————————————————————————


# 2. 调用model.parameters()可以得到第一线性模块和第二线性模块中的权重和偏差。
## 在本例中，我们可以通过打印形状来检查参数：
[param.shape for param in seq_model.parameters()]

## 输出
[torch.Size([13, 1]), torch.Size([13]), torch.Size([1, 13]), torch.Size([1])]
# ——————————————————————————————————————————————————————————————————

# 3. 当你检查由几个子模块组成的模型的参数时，可以方便地通过其名称识别参数。这个方法叫做named_parameters
for name, param in seq_model.named_parameters():
    print(name, param.shape)

##  输出
0.weight torch.Size([13, 1])
0.bias torch.Size([13])
2.weight torch.Size([1, 13])
2.bias torch.Size([1])