Image Warping

图像扭曲是计算机视觉和图像处理中的一个重要概念，它涉及到改变图像的几何形状或位置，使其看起来像是被拉伸、压缩或旋转。

Reference materials include:

• C0S 426, Fall 2000
• C0S 426, Spring 2022
• Resampling filters

基础知识

图像预处理操作包括五大类内容。

• Quantization: 量化是将连续的像素值（或颜色值）转换为离散的级别。这个过程在图像压缩和图像格式转换中非常常见。
  • Uniform Quantization
  • Random dither
  • Ordered dither
  • Floyd-Steinberg dither
• Pixel operations: 像素操作是对图像中的每个像素值进行独立处理，通常不考虑像素之间的关系。
  • Add random noise
  • Add luminance
  • Add contrast
  • Add saturation
• Filtering: 滤波是通过卷积操作处理图像，考虑一个像素及其邻域像素的关系，用于平滑图像或增强特定特征。
  • Blur
  • Detect edges
• Warping: 图像扭曲涉及对图像进行几何变换，改变其形状或位置。
  • Scale
  • Rotate
  • Warp
• Combining: 组合是将多幅图像或图像的不同部分合成一幅新的图像。
  • Composite
  • Morph
    总之，图像预处理的目标是通过一系列的操作来改善图像质量、增强特定特征、减少噪声或校正几何畸变等，为后续的高级图像处理和计算机视觉任务奠定基础。这些技术在图像预处理阶段共同作用，确保输入到后续步骤的图像数据是最优化的。

而在图像处理过程中，空间图像的几何变换包括两个主要步骤：映射（mapping）和重采样（resampling）。这两个步骤是实现图像扭曲、变换或几何校正的关键。

• Move pixels of image
  • Mapping ：空间坐标变换关系
    • Forward
    • Inverse
  • Resampling ：变换坐标的赋值、插值运算
    • Point sampling
    • Triangle filter
    • Gaussian filter

Mapping

映射是确定图像中每个像素在变换后的新位置。它定义了从原始图像到目标图像的坐标变换关系。这个过程主要关注的是计算像素如何从原始位置移动到新的位置。

Define transformation

Describe the destination (x,y) for every location (u,v) in the source (or vice-versa, if invertible).

Example Mappings

变换函数可以是仿射变换、透视变换或其他非线性变换。

• 仿射变换（Affine Transformation）：是一类保持点、直线和线段平行性的变换。它包括：

  • 线性变换（如旋转-Rotate、缩放-Scale、剪切-Shear）
  • 平移-Translation

• 透视变换 （Perspective Transformation）：是用于模拟三维视角效果、图像校正和增强现实的变换。透视变换是一种保留直线性质的变换。它能够将直线投影成直线，但不保持平行性，适合处理远近关系。

• 将三维空间中的点投影到二维平面上

• 逆向透视变换 (Inverse Perspective Mapping)：将二维图像中的点映射回三维空间。常用于图像校正、如车道线检测、摄像头标定等

• 非线性变换 （Non-linear Transformation）：非线性变换通常没有固定的公式，可以是任意函数。

• 径向变换（Radial Transformation）：用于校正镜头的径向畸变，如桶形畸变和枕形畸变。

• 极坐标变换：常用于全景图像处理和纹理映射。

• 涡旋变换-Swirl：将图像进行旋转扭曲，常用于图像特效。

• 波浪变换-Wave Transformation：用于模拟波浪效果。

• Rain：雨效应是一种通过在图像上叠加模拟雨滴的效果来生成下雨场景的技术

• 弹性变形（Elastic Deformation）：弹性变形常用于数据增强。通过在图像上应用随机的、局部的位移场来实现，这些位移场通常由高斯滤波器平滑处理后生成，从而生成具有更大多样性的数据集。

• 双曲线变换（Hyperbolic Transformation）：用于创建各种扭曲和形变效果

• Fish-eye：模拟鱼眼镜头效果的非线性变换，使得图像中心区域被放大，而边缘区域被压缩，产生一种球形的视觉效果，属于桶形畸变。

• 光流变换：用于追踪图像序列中的运动，用于视频处理和运动分析

• 图像网格变形（Mesh Warp Transformation）：通过在图像上定义控制点和网格，调整控制点来实现变形

• Thin Plate Spline：平滑变形，特别是在图像配准和形状匹配中

Image Warping Implementation

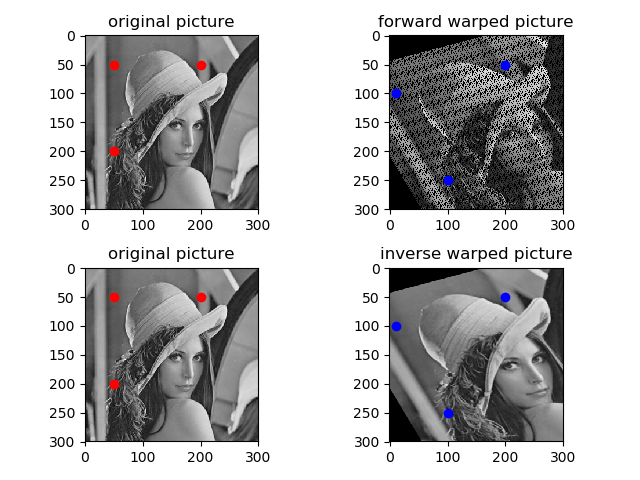
逆向映射（inverse mapping）通常比前向映射（forward mapping）更有效，主要原因有以下几点：

1. forward mapping从源图像空间出发，逐个像素地将其映射到目标图像中。这个过程中，可能会出现一些目标图像像素没有被任何源图像像素映射到，导致空洞问题，需要额外的插值或其他处理方法来填补这些空洞。
2. inverse mapping从目标图像空间出发，逐个像素地寻找其在源图像中的对应位置。这样可以确保目标图像的每个像素都被处理到，避免出现空洞（holes）或未填充的像素。

# Forward mapping
## Iterate over source image
### Many source pixels can map to same destination pixel
### Some destination pixels may not be covered

for (int u = 0; u < umax; u++) {
    for (int v = 0; v < vmax; v++) {
        float x = fx(u,v);
        float y = fy(u,v);
        dst(x,y) = src(u,v);
        }
    }

# Reverse mapping
## Iterate over destination image 
### Must resample source 
### May oversample, but much simpler!
for (int x = 0; x < xmax; x++) {
    for (int y = 0; y < ymax; y++) {
        float u = fx^-1(x,y);
        float v = fy^-1(x,y);
        dst(x,y) = src(u,v);
        }
    }

Resampling

Evaluate source image at arbitrary (u,v), (u,v) does not usually have integer coordinates.=》重采样是将映射得到的新位置的像素值进行填充。由于映射后的坐标（x’, y’）通常不是整数坐标，因此需要对这些坐标进行插值以获得最终的像素值。

Resampling Artefacts

1. Blocking

   The primary cause of ‘blocking’ is either badly anti-aliased source image, or not enough smoothing (color mixing or blurring) between pixels to improve the overall look of an image.

2. Ringing

   Ringing is an effect you often see in very low quality JPEG images close to sharp edges. It is typically caused by an edge being over compensated for by the resize or image compression algorithm, or a high quality filter being used with a bad support size.

3. Aliasing and Moiré Effects

   Aliasing effects are generally seen as the production of ‘staircase’ like effects along edges of images.

4. Blurring

香农采样定理

在实现移动像素的操作时，必须考虑到数字图像是连续图像的采样版本。Sampling是从连续函数中采样离散样本。Reconstrution是从离散样本恢复连续函数。

采样点太少会发生Aliasing: high frequencies masquerade as low ones。具体而言，会发生Spatial aliasing（due to limited spatial resolution）、Temporal aliasing（ due to limited temporal resolution）和Missing Image Detail.

Sampling rate must be > 2 bandwidth.

• That frequency is called the bandwidth
• The minimum sampling rate for a bandlimited function is called the “Nyquist rate”
• Shannon: A signal can be reconstructed from its samples iff it has no content ≥ ½ the sampling frequency：只有当信号的频率成分全部低于采样频率的一半（奈奎斯特频率）时，才能从采样中完整重建信号。

香农采样定理里面提到“采样频率等于有效信号频率的两倍”很关键。如果我们采样的频率过慢，就会导致有多条函数经过采样点进而导致采样点对应的时序函数结果不唯一，所以要提高采样频率。

香农采样定理跟图像的联系是自然而然的。图像本身也是现实世界在计算机中的一种离散表示，所以图像在经过傅里叶变换之后能够被表示为某种时域函数（一堆正弦或余弦函数的叠加），那图像处理中的香农采样定理，就可以表示为：当我们使用高于最高频率2倍的频率对图像进行采样时，能够正确完整的复原图像。

Resample = Reconstruct + Transform + Filter + Sample. 重新采样过程中往往通过卷积操作平滑信号或图像，滤除高频成分，防止伪影的产生，从而实现有效的重新采样。

• What is done is to try to use some type of weighted average of the original source pixel values to determine a good value for the new pixel. The real pixels surrounding the location of the new pixel forms a ‘neighbourhood’ of contributing values. The larger this neighbourhood is the slower the resize. This is a technique called Convolution.

Sampling operation

Point sampling

Interpolation is usually only used for ‘point’ sampling images, when image scaling is either not known or needed. For example, when rotating image or minor distortions, the image’s scaling or size does not change, and as such an interpolation can produce a reasonable result, though not a very accurate one.

Take value at closest pixel: This method is simple, but it causes Aliasing and Moiré Effects.

• Box: just directly averaging the nearby pixels together

Triangle filter

The ‘Triangle‘ or ‘Bilinear‘ interpolation filter just takes the interpolation of the nearest neighbourhood one step further, it weights them according to how close the new pixels position is to the the original pixels within the neighbourhood (or ‘support‘ region). The closer the new pixel is to a source image pixel, the more color that pixel contributes.

Convolve with triangle filte: Bilinearly interpolate four closest pixels.

Other Interpolated Filters

• Hermite
• Lagrange
• Catrom (Catmull-Rom) filter is a well known standard Cubic Filter often used as an interpolation function

Gaussian filter

Convolve with Gaussian filter: Compute weighted sum of pixel neighborhood.

• Gaussian Interpolator Filter Variant

Image Warping Implementation

Reverse mapping:
for (int x = 0; x < xmax; x++) {
	for (int y = 0; y < ymax; y++) {
		float u = fx^-1(x,y);
		float v = fy^-1(x,y);
		dst(x,y) = resample_src(u,v,w);
	}
}